アンドロメダ銀河に近づくポン・ブルックス彗星 ― 2024/03/10
昨宵は良い天気でしたが、風が少し残っていたので長焦点ではなく短焦点でポン・ブルックス彗星(12P)を狙ってみました。ちょうど70mm-80mm+APS-Cでアンドロメダ銀河(M31)と一緒に収まりました。
左画像はまだ薄明が残っており、地上の光害もきつい時間帯での撮影です。中央右上寄りにM31、中央に対してM31と対象位置に彗星がいます。彗星から短い尾がM31の方向に伸びていますね。空の条件が良い場所で撮影すると、例えばSpaceWeather.com3月7日記事表紙のようにM31に届くほどの尾になっているようですね。でも市街地の薄汚れた空ではこれが精いっぱい。
自分の眼で見たかったということもありますが、それよりも「普段の生活に居ながら、肉眼で彗星の尾やアンドロメダ銀河が見えるような素晴らしい環境」を後世に残せないことが何よりも残念でなりません。「山奥に出かければ…」とか「海外に行けば…」といった天文環境の封じ込めが続く限り、数世代後のこどもたちにとって宇宙はパソコン画面を通してしか見ることができない「非日常の事象」になってしまうことでしょう。
約一ヶ月後の4月10日宵には、この画像と同程度の画角にポン・ブルックス彗星、木星、極細月、天王星が全て入ります。高度15°以下の低空ですが、彗星は計算上で今より2等ほど明るく、最大光度期の約10日前ですから肉眼で感じ取れるかも知れません。小型双眼鏡を片手に、ぜひ眺めてみてください。
左画像はまだ薄明が残っており、地上の光害もきつい時間帯での撮影です。中央右上寄りにM31、中央に対してM31と対象位置に彗星がいます。彗星から短い尾がM31の方向に伸びていますね。空の条件が良い場所で撮影すると、例えばSpaceWeather.com3月7日記事表紙のようにM31に届くほどの尾になっているようですね。でも市街地の薄汚れた空ではこれが精いっぱい。
自分の眼で見たかったということもありますが、それよりも「普段の生活に居ながら、肉眼で彗星の尾やアンドロメダ銀河が見えるような素晴らしい環境」を後世に残せないことが何よりも残念でなりません。「山奥に出かければ…」とか「海外に行けば…」といった天文環境の封じ込めが続く限り、数世代後のこどもたちにとって宇宙はパソコン画面を通してしか見ることができない「非日常の事象」になってしまうことでしょう。
約一ヶ月後の4月10日宵には、この画像と同程度の画角にポン・ブルックス彗星、木星、極細月、天王星が全て入ります。高度15°以下の低空ですが、彗星は計算上で今より2等ほど明るく、最大光度期の約10日前ですから肉眼で感じ取れるかも知れません。小型双眼鏡を片手に、ぜひ眺めてみてください。
イブに月とすばるが急接近 ― 2023/12/25
クリスマスイブの昨宵はサンタこそ見かけませんでしたが、北空高く通過するスターリンク・トレイン(Group6-32)が見えました。青くて綺麗でしたが、光害や大気汚染、宇宙デブリの元になると考えると悩ましい…。登ったばかりの月がプレアデス星団(すばる)に接近して素晴らしい眺めでした。まもなく満月ということもあってさすがのプレアデス星団も霞んでいたけれど、明るい星団トップ3に名を連ねるほどですから双眼鏡で一緒に見える事実だけでも十分驚きます。
最接近瞬時は24日17:21ごろでした。このときの離角は約1.564°。最接近離角が2.0°を下回り始めたのは今年6月からで、今回は月が星団の南を通過する形です。当地ではまだ東の電線群の中でしたので、月の観察を終えた20時過ぎに左上画像を撮影。ふつうに撮影すると月も空も白飛びするため、4段階の多段階露光で月面も月周囲の微光星もなるべく取り出してあります。とは言え、満月期は難しいですね。流行りの生成AIででっち上げような絵面になってしまいます。
月とプレアデス星団の接近は緩やかな周期性があります。これは他の月に絡む接近/掩蔽現象…例えばアンタレス掩蔽やアルデバラン掩蔽、あるいは日食なども同じ理屈で、月の軌道面(白道面)が黄道面に対してゆっくり動いていることが大きな要因です。月軌道面は概ね黄道に近いですが、もし完全に同じなら毎周回ごと同じ天体に同じ離角で接近しますから、遠近の変化は起こりません。でも実際はわずかに異なり、しかもすりこぎ運動をしています(→国立天文台・暦wiki解説参照)。
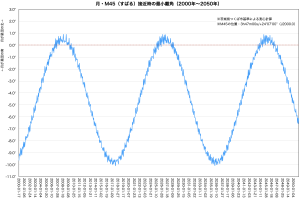
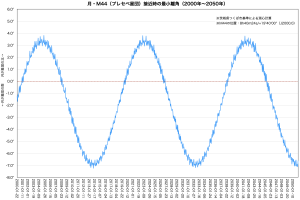
下A・B図としてM45(プレアデス星団)およびM44(プレセペ星団)との離角を50年分示しました。「月が各天体に一番近い日時ごとに離角をプロットしたもの」という図です。離角は通常正の値のみですが、この図では「月が星団の南を通過する場合はマイナス値」として、南北位置関係も表現しています。また現実に則するため測心計算にしました。月は近い天体ですから地心計算と測心計算とでかなり異なり、また自転の影響を受けないので滑らかな曲線になります。
今はプレアデス星団の南側をスルーしている月も、2025年ごろには星団のなかにどっぷり浸かり始めるでしょう。今週29日夜中ごろに接近するプレセペ星団も北に離れているけれど、2026年ごろから星団を隠す様子が見られます。楽しみですね。
月面の拡大観察もしました。前夜ほどではありませんがシーイングは3/10とまずまず。ただし宵なのに既に2度を下回る気温になり辛かったです。撮影した中から3枚掲載。
下C画像はすっかり明るくなった虹の入り江付近。リッジはあまり浮き出なくなり、リム近くの山々だけが目立ちます。J.ハーシェルの奥、たぶんアナクシマンデルやサウスなどのクレーター壁だけが紐状に光り、やたら明るく感じました。前夜に見えなかったグルイテュイゼン・ガンマの山頂付近にある小クレーターをやっと確認。
下D画像は光条が目立ってきたコペルニクスから明暗境界にかけて。欠け際にアリスタルコスとヘロドトスのコンビ。左下にマリウスも見えています。ブツブツが出始めましたね。マリウス谷が白い糸状に見えています。前夜見えたドリル山のギザギザは見えなくなりました。
下E画像はすっかり明るいシラー付近。シラー・ズッキウス・ベイスンの凹みが感じられます。欠け際にシッカルトが見え始めていました。シッカルトでのRay現象というのは耳にしませんが、クレーターの低い縁から幅広の光線がなだれ込み、少しずつ明るくなっていました。右画像は18:40と19:19に同じエリアを撮影したトリミング組み写真ですが、たった40分でこんなに変わります。広い意味ではこれもRay現象ですね。またシーイングが尻上がりに良くなった様子も分かるでしょう。
最接近瞬時は24日17:21ごろでした。このときの離角は約1.564°。最接近離角が2.0°を下回り始めたのは今年6月からで、今回は月が星団の南を通過する形です。当地ではまだ東の電線群の中でしたので、月の観察を終えた20時過ぎに左上画像を撮影。ふつうに撮影すると月も空も白飛びするため、4段階の多段階露光で月面も月周囲の微光星もなるべく取り出してあります。とは言え、満月期は難しいですね。流行りの生成AIででっち上げような絵面になってしまいます。
月とプレアデス星団の接近は緩やかな周期性があります。これは他の月に絡む接近/掩蔽現象…例えばアンタレス掩蔽やアルデバラン掩蔽、あるいは日食なども同じ理屈で、月の軌道面(白道面)が黄道面に対してゆっくり動いていることが大きな要因です。月軌道面は概ね黄道に近いですが、もし完全に同じなら毎周回ごと同じ天体に同じ離角で接近しますから、遠近の変化は起こりません。でも実際はわずかに異なり、しかもすりこぎ運動をしています(→国立天文台・暦wiki解説参照)。
下A・B図としてM45(プレアデス星団)およびM44(プレセペ星団)との離角を50年分示しました。「月が各天体に一番近い日時ごとに離角をプロットしたもの」という図です。離角は通常正の値のみですが、この図では「月が星団の南を通過する場合はマイナス値」として、南北位置関係も表現しています。また現実に則するため測心計算にしました。月は近い天体ですから地心計算と測心計算とでかなり異なり、また自転の影響を受けないので滑らかな曲線になります。
今はプレアデス星団の南側をスルーしている月も、2025年ごろには星団のなかにどっぷり浸かり始めるでしょう。今週29日夜中ごろに接近するプレセペ星団も北に離れているけれど、2026年ごろから星団を隠す様子が見られます。楽しみですね。
月面の拡大観察もしました。前夜ほどではありませんがシーイングは3/10とまずまず。ただし宵なのに既に2度を下回る気温になり辛かったです。撮影した中から3枚掲載。
下C画像はすっかり明るくなった虹の入り江付近。リッジはあまり浮き出なくなり、リム近くの山々だけが目立ちます。J.ハーシェルの奥、たぶんアナクシマンデルやサウスなどのクレーター壁だけが紐状に光り、やたら明るく感じました。前夜に見えなかったグルイテュイゼン・ガンマの山頂付近にある小クレーターをやっと確認。
下D画像は光条が目立ってきたコペルニクスから明暗境界にかけて。欠け際にアリスタルコスとヘロドトスのコンビ。左下にマリウスも見えています。ブツブツが出始めましたね。マリウス谷が白い糸状に見えています。前夜見えたドリル山のギザギザは見えなくなりました。
下E画像はすっかり明るいシラー付近。シラー・ズッキウス・ベイスンの凹みが感じられます。欠け際にシッカルトが見え始めていました。シッカルトでのRay現象というのは耳にしませんが、クレーターの低い縁から幅広の光線がなだれ込み、少しずつ明るくなっていました。右画像は18:40と19:19に同じエリアを撮影したトリミング組み写真ですが、たった40分でこんなに変わります。広い意味ではこれもRay現象ですね。またシーイングが尻上がりに良くなった様子も分かるでしょう。
2023年の秋分を迎えました ― 2023/09/23
本日は2023年の秋分です。我が家の周囲は昨日から続く雨でしっとり。気温もぐっと下がり、朝9時時点で肌寒さを感じたのは夏以降初めてでした。このまま平年並に落ち着いてくれると良いのですが…。
2020年に閏年を迎えてから、今年で4回目の秋。太陽位置を基準に決める二十四節気の日時は、「閏年の周期」すなわち「4年ごとに1日追加」という変化がダイレクトに影響します。閏日よりあとにやって来る秋分などの節気は、閏年前年に対して18時間あまり早まり、その後3年間かけて6時間弱ずつ遅くなります。こうしてなるべく一定期間に収まるよう工夫している訳ですね。
右下図は当ブログで時々掲載してきた二十四節気の日時変化。今回は秋分の変化の図です。来年は閏年なのでまた早まって、なんと128年前の1896年9月22日22:03:41という記録より早い秋分を迎えることになるでしょう。しばらくは4年ごとに最早記録が更新されます。でも過去には1796年22日17:24:02、さらにその前には1696年22日12:08:17という最早記録が控えていますから、これを更新するのはあと50年くらいかかりそうですね。
夏が異様に暑かったためか、窓下にひっそり生えている彼岸花は昨日やっと開花した状態。例年なら秋分の日に半数ほど咲き終えて枯れてる状態なので、大幅に遅れています。目立つ桜や彼岸花だけでなく、気候が大きく変化した際に遅れたり早まったりする植物は極めて多いことでしょう。更にその植物に依存する動物にも影響が及びます。人間も今は流通や加工保存の技術があるから多くの場合で食料難に陥らず持ちこたえているけれど、食料確保が個人に委ねられることになったら生き延びられないでしょうね。
閏日の仕組みを作り、ちまちまと日時管理しているのが馬鹿らしく思えるほど、自然界の「ずれ」や「崩れ」が大きくなっている気がします。多分これは人の叡知でどうにかできるものではないのでしょう。
2020年に閏年を迎えてから、今年で4回目の秋。太陽位置を基準に決める二十四節気の日時は、「閏年の周期」すなわち「4年ごとに1日追加」という変化がダイレクトに影響します。閏日よりあとにやって来る秋分などの節気は、閏年前年に対して18時間あまり早まり、その後3年間かけて6時間弱ずつ遅くなります。こうしてなるべく一定期間に収まるよう工夫している訳ですね。
右下図は当ブログで時々掲載してきた二十四節気の日時変化。今回は秋分の変化の図です。来年は閏年なのでまた早まって、なんと128年前の1896年9月22日22:03:41という記録より早い秋分を迎えることになるでしょう。しばらくは4年ごとに最早記録が更新されます。でも過去には1796年22日17:24:02、さらにその前には1696年22日12:08:17という最早記録が控えていますから、これを更新するのはあと50年くらいかかりそうですね。
夏が異様に暑かったためか、窓下にひっそり生えている彼岸花は昨日やっと開花した状態。例年なら秋分の日に半数ほど咲き終えて枯れてる状態なので、大幅に遅れています。目立つ桜や彼岸花だけでなく、気候が大きく変化した際に遅れたり早まったりする植物は極めて多いことでしょう。更にその植物に依存する動物にも影響が及びます。人間も今は流通や加工保存の技術があるから多くの場合で食料難に陥らず持ちこたえているけれど、食料確保が個人に委ねられることになったら生き延びられないでしょうね。
閏日の仕組みを作り、ちまちまと日時管理しているのが馬鹿らしく思えるほど、自然界の「ずれ」や「崩れ」が大きくなっている気がします。多分これは人の叡知でどうにかできるものではないのでしょう。
超高層雷放電「スプライト」を撮る ― 2023/09/06
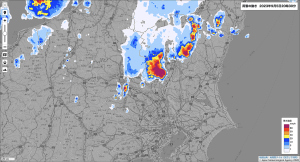
昨宵から夜にかけて、当地・茨城県南部の北西に位置する栃木県南部を中心に発達した積乱雲が夜空を照らしていました(左図/気象庁・降水ナウキャストから引用)。当地は良く晴れており雷雲もこちらへは来ないようなので、発光現象「スプライト」を写せるかどうかやってみました。
雷(稲妻)は主に積乱雲の中や地面との間で起こる発光です。でも大きく発達した積乱雲では雲の上に向かう稲妻(右下画像/2015年8月5日撮影)や、その他の発光も起きることがあります。「その他の発光」として一番知られているのが「スプライト」という現象です。
大気層は大きく四種に分類され、地面から上に向かってそれぞれ対流圏(troposphere:10km以下)、成層圏(stratosphere:10km以上)、中間圏(mesosphere:50km以上)、熱圏(thermosphere:80km以上)と呼ばれます。積乱雲の上層は成層圏下部まで達しますから、それより上で起こる発光は「超高層雷放電」と表現され、様々なタイプの現象が知られています。スプライトの呼び名が広義に解釈されて超高層雷放電を指すこともあるようですが、狭義にはカツオノエボシ系のクラゲの足みたいな赤い発光のみを指します。規模の大きなスプライトは熱圏下層に到達するそうなので、想像を絶する大きさですね。ちなみに一般的な「地球と宇宙の境界」は100kmで、流れ星はそれよりずっと下で光ります。スプライトなどの大規模な超高層雷放電は国際宇宙ステーションからも見えるそうです。
さて、昨夜は簡易的な白黒カメラによる約2時間の観察で、5シーンの発光を記録できました(下A…E画像)。通常この手の撮影は高感度カメラの動画記録が定石なのですが、ミリ秒オーダーの発光を動画で追うと容量も膨れ上がり、見返すのも大変な作業です。要は暗い流星の撮影と同じですから、今回は5秒露出の高感度静止画で記録しました。またスプライトは赤い波長なので、光害カットを兼ねて近赤外透過フィルターを付けています。
下画像の背景にはうしかい座やかんむり座、おおぐま座などが写っています。ちょうど撮影準備中、前日に打ち上げられたばかりのStarlinkトレイン(Group6-12)が、画像右寄りに写ってる北斗七星の柄のあたりから頭上へ向かって通過してゆき、たいへん明るくて驚きました。5分早く撮影スタートしていたら写っていたでしょう。左下のカーブした光は地上光のゴースト。画像のうちBとCはスプライトではなくジェットかも知れません。色情報が無いから何とも判断できないけれど、他写真のスプライトとは明らかに形状が違います。
背景に星が写っていると、撮影時刻が分かればスプライトの最高点仰角を測ることができます。今回は少なくとも約35°まで届いていました。正確なスプライト発生位置は分かりませんが、自宅から約100km先に雷雲中心があったので、地面の曲率を無視して100×tan(35°)=70とし、このスプライトは地表からみて70kmあたりまで達していたと推測できます。複数点で同じ雷雲のスプライトを捉えれば、より精度の高い計算も可能でしょう。流星経路の計算と同じですね。
スプライトを撮ってみたいという方は、流星撮影の基本的な知識、機材選定、天気判断の知識があると良いでしょう。自身の観察地が雷になっている必要はなく、むしろ自身の居場所は快晴なのに100kmから200km程度離れたところで強い雷雨になっている状況(雷雲が自分のほうへ来ないことが前提)を狙ってください。もちろん薄暮・薄明も無い夜時間でないときれいに写りません。近い雷雲ほどスプライトも高くなり、縦方向の写野にゆとりがあるレンズが必要です。雷雲の広がりにも寄りますが、縦構図のほうが良いかも知れません。SpaceWeather.comの特集記事の下にある図を参考に、雷雲までの距離と必要な画角を計算して一覧表を作っておきましょう。
実はこれまで何回も挑戦していたのですが、なかなか良いタイミングに巡り合えませんでした。薄暮が終わるころ雷も下火になってしまったり、鉄床雲の広がりが大き過ぎて自分の街まで飲み込まれたり…。茨城は西で発生した雷が発達しながら通過することが多いため、撮影する間もなく落雷被害を受けてしまうほうが圧倒的に多いのです。事故は十二分に気を付けなくてはなりません。もし運良く次のチャンスが巡ってきたら、カラー撮影をしてみたいと思います。
雷(稲妻)は主に積乱雲の中や地面との間で起こる発光です。でも大きく発達した積乱雲では雲の上に向かう稲妻(右下画像/2015年8月5日撮影)や、その他の発光も起きることがあります。「その他の発光」として一番知られているのが「スプライト」という現象です。
大気層は大きく四種に分類され、地面から上に向かってそれぞれ対流圏(troposphere:10km以下)、成層圏(stratosphere:10km以上)、中間圏(mesosphere:50km以上)、熱圏(thermosphere:80km以上)と呼ばれます。積乱雲の上層は成層圏下部まで達しますから、それより上で起こる発光は「超高層雷放電」と表現され、様々なタイプの現象が知られています。スプライトの呼び名が広義に解釈されて超高層雷放電を指すこともあるようですが、狭義にはカツオノエボシ系のクラゲの足みたいな赤い発光のみを指します。規模の大きなスプライトは熱圏下層に到達するそうなので、想像を絶する大きさですね。ちなみに一般的な「地球と宇宙の境界」は100kmで、流れ星はそれよりずっと下で光ります。スプライトなどの大規模な超高層雷放電は国際宇宙ステーションからも見えるそうです。
さて、昨夜は簡易的な白黒カメラによる約2時間の観察で、5シーンの発光を記録できました(下A…E画像)。通常この手の撮影は高感度カメラの動画記録が定石なのですが、ミリ秒オーダーの発光を動画で追うと容量も膨れ上がり、見返すのも大変な作業です。要は暗い流星の撮影と同じですから、今回は5秒露出の高感度静止画で記録しました。またスプライトは赤い波長なので、光害カットを兼ねて近赤外透過フィルターを付けています。
下画像の背景にはうしかい座やかんむり座、おおぐま座などが写っています。ちょうど撮影準備中、前日に打ち上げられたばかりのStarlinkトレイン(Group6-12)が、画像右寄りに写ってる北斗七星の柄のあたりから頭上へ向かって通過してゆき、たいへん明るくて驚きました。5分早く撮影スタートしていたら写っていたでしょう。左下のカーブした光は地上光のゴースト。画像のうちBとCはスプライトではなくジェットかも知れません。色情報が無いから何とも判断できないけれど、他写真のスプライトとは明らかに形状が違います。
背景に星が写っていると、撮影時刻が分かればスプライトの最高点仰角を測ることができます。今回は少なくとも約35°まで届いていました。正確なスプライト発生位置は分かりませんが、自宅から約100km先に雷雲中心があったので、地面の曲率を無視して100×tan(35°)=70とし、このスプライトは地表からみて70kmあたりまで達していたと推測できます。複数点で同じ雷雲のスプライトを捉えれば、より精度の高い計算も可能でしょう。流星経路の計算と同じですね。
スプライトを撮ってみたいという方は、流星撮影の基本的な知識、機材選定、天気判断の知識があると良いでしょう。自身の観察地が雷になっている必要はなく、むしろ自身の居場所は快晴なのに100kmから200km程度離れたところで強い雷雨になっている状況(雷雲が自分のほうへ来ないことが前提)を狙ってください。もちろん薄暮・薄明も無い夜時間でないときれいに写りません。近い雷雲ほどスプライトも高くなり、縦方向の写野にゆとりがあるレンズが必要です。雷雲の広がりにも寄りますが、縦構図のほうが良いかも知れません。SpaceWeather.comの特集記事の下にある図を参考に、雷雲までの距離と必要な画角を計算して一覧表を作っておきましょう。
実はこれまで何回も挑戦していたのですが、なかなか良いタイミングに巡り合えませんでした。薄暮が終わるころ雷も下火になってしまったり、鉄床雲の広がりが大き過ぎて自分の街まで飲み込まれたり…。茨城は西で発生した雷が発達しながら通過することが多いため、撮影する間もなく落雷被害を受けてしまうほうが圧倒的に多いのです。事故は十二分に気を付けなくてはなりません。もし運良く次のチャンスが巡ってきたら、カラー撮影をしてみたいと思います。