月・水星・金星が作る三角形 ― 2020/05/25
昨日は午後までずっと曇り空。時々日が差したのですが、太陽撮影できるほどではありませんでした。ところが、夕方が近づくにつれて青空が広がってきたではありませんか。こうなると前々から楽しみにしていた「金星・水星・月の接近」が見えるかも知れません。
日が暮れて30分もしないうちに3天体が西空低く輝き出しました。金星は6月4日の内合に向けてぐんぐん太陽に近づいており、もう水星より低くなっています。3天体は小さく整った三角形に並び、可愛らしく感じました(左画像)。よく見ると金星が欠けているのも分かりますね。
元々低い位置での現象なので暗くなるのを待つ時間はありません。日没後から少し雲が湧いてしまいましたが、それでも20分ほど楽しむことができ、ほどなく星たちは低空の街並みに消えてゆきました。もう少し高かったら良かったんだけど…。
さて、このシーンをご覧になった方でもあまり気が付かなかったでしょうが、実は月・水星・金星が作る形として非常に稀な「極めて正三角形に近い形」でした。もちろん日没後に撮影した左上画像を見てもそんなふうに見えませんが、約3時間前の16時頃の位置は右図の様だったんです(Stellariumによる作画/赤道座標系で表示)。
各天体がどう動いてこの形になったか、というところまで頭に入ってないと、本来青空の中で見えるであろうこの正三角形の配置は想像できませんね。
時として天体の配列は驚くほど整った形を見せてくれます。正三角形でいうと、大きいものでは「冬の大三角形」がそうでしょう。小さいものでは、こと座の「α・ε・ζ」とか、へび座頭部の「β・γ・κ」が作る三角なども健闘してますよね。もちろん実際は天球というスクリーン上の「球面三角」ですが、今回は細かい事抜きに平面の話として進めましょう。恒星のアステリズムは惑星のように位置が変わりませんから、いつでも楽しめるでしょう。逆に言うと、複雑な運動をする惑星が綺麗に並ぶって、どれほどすごい偶然なんだろうと感心してしまったわけです。
実際に月・水星・金星が正三角形に近い形になる機会がどれくらいあるのか、自作プログラムを組んで2000年以降50年ほど計算してみました。結果は左表のとおり。かなり少ないけれど、チャンスはあるのですね(※ただし日本で見えるとは限りません)。
ここで言う「差分率」は“正三角らしさ”を当記事で勝手に定義した計算値。「一番長い辺と一番短い辺の差が、各辺平均の何%か」を求めています。統計学の偏差とは関係ありません。当然ながら正三角形に近いほどゼロに近づきます。参考までに恒星アステリズムの差分率もいくつか計算し、以下に掲載しました。併せて比較してみましょう。
表を見てお分かりのように、昨夕のケースは他の例より文字通り“桁違い”に小さな数値でした。異例と言えるほど正三角形に近かったわけですね。日本より3時間前に日が沈んでいたマーシャル諸島の浜辺ではさぞ美しい形が見えただろうと想像しただけでゾクゾクしませんか?
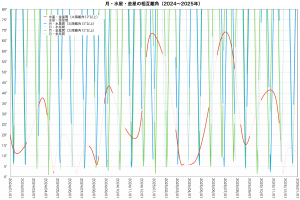
月は一ヶ月かけて天球を一周しますから、毎月のように水星や金星と接近します。でも水星と金星が接近するのはそれほど頻繁ではありません(下図参照)。その上、各天体が全て太陽から離れて見やすい位置にいる、とか、離角が均等になって正三角形になっている、といったたくさんの偶然が重なって、昨夕のシーンが生まれました。なんでもないときにふと自然が一瞬だけ奏でるハーモニー。これを見逃さない目、聞き逃さない耳を養うことは難しく、そしてとても大切に思います。
参考:
月・金星・木星の接近はなかなか起こらない(2017/11/17)
アーカイブ:2015年1月の金星と水星接近に関係する記事(ブログ内)
日が暮れて30分もしないうちに3天体が西空低く輝き出しました。金星は6月4日の内合に向けてぐんぐん太陽に近づいており、もう水星より低くなっています。3天体は小さく整った三角形に並び、可愛らしく感じました(左画像)。よく見ると金星が欠けているのも分かりますね。
元々低い位置での現象なので暗くなるのを待つ時間はありません。日没後から少し雲が湧いてしまいましたが、それでも20分ほど楽しむことができ、ほどなく星たちは低空の街並みに消えてゆきました。もう少し高かったら良かったんだけど…。
さて、このシーンをご覧になった方でもあまり気が付かなかったでしょうが、実は月・水星・金星が作る形として非常に稀な「極めて正三角形に近い形」でした。もちろん日没後に撮影した左上画像を見てもそんなふうに見えませんが、約3時間前の16時頃の位置は右図の様だったんです(Stellariumによる作画/赤道座標系で表示)。
各天体がどう動いてこの形になったか、というところまで頭に入ってないと、本来青空の中で見えるであろうこの正三角形の配置は想像できませんね。
時として天体の配列は驚くほど整った形を見せてくれます。正三角形でいうと、大きいものでは「冬の大三角形」がそうでしょう。小さいものでは、こと座の「α・ε・ζ」とか、へび座頭部の「β・γ・κ」が作る三角なども健闘してますよね。もちろん実際は天球というスクリーン上の「球面三角」ですが、今回は細かい事抜きに平面の話として進めましょう。恒星のアステリズムは惑星のように位置が変わりませんから、いつでも楽しめるでしょう。逆に言うと、複雑な運動をする惑星が綺麗に並ぶって、どれほどすごい偶然なんだろうと感心してしまったわけです。
【月・水星・金星の作る正三角形】
| 日時 | 月・水星・金星の離角 | 差分率 |
|---|---|---|
| 2003年5月29日 6:00 | 2.80° ・ 3.08° ・ 2.60° | 17.1% |
| 2011年10月28日 15:00 | 2.18° ・ 1.94° ・ 2.11° | 11.9% |
| 2016年2月6日 18:00 | 5.23° ・ 4.45° ・ 4.83° | 16.1% |
| 2020年5月24日 15:00 | 3.83° ・ 3.81° ・ 3.89° | 2.2% |
| 2022年12月25日 0:00 | 4.53° ・ 3.85° ・ 4.33° | 16.0% |
| 2031年7月22日 6:00 | 3.09° ・ 2.62° ・ 2.65° | 16.8% |
| 2035年6月5日 6:00 | 3.53° ・ 3.78° ・ 4.19° | 17.2% |
| 2038年8月29日 15:00 | 2.59° ・ 3.29° ・ 2.90° | 23.7% |
| ||
ここで言う「差分率」は“正三角らしさ”を当記事で勝手に定義した計算値。「一番長い辺と一番短い辺の差が、各辺平均の何%か」を求めています。統計学の偏差とは関係ありません。当然ながら正三角形に近いほどゼロに近づきます。参考までに恒星アステリズムの差分率もいくつか計算し、以下に掲載しました。併せて比較してみましょう。
- 冬の大三角…5.36%
- 春の大三角…7.35%
- 夏の大三角…44.24%
- こと座α-ε1-ζ1…20.21%
- へび座頭部β-γ-κ…21.89%
- カシオペア座α-β-γ…27.93%
- さんかく座α-β-γ…93.93%
- みなみのさんかく座α-β-γ…22.50%
表を見てお分かりのように、昨夕のケースは他の例より文字通り“桁違い”に小さな数値でした。異例と言えるほど正三角形に近かったわけですね。日本より3時間前に日が沈んでいたマーシャル諸島の浜辺ではさぞ美しい形が見えただろうと想像しただけでゾクゾクしませんか?
月は一ヶ月かけて天球を一周しますから、毎月のように水星や金星と接近します。でも水星と金星が接近するのはそれほど頻繁ではありません(下図参照)。その上、各天体が全て太陽から離れて見やすい位置にいる、とか、離角が均等になって正三角形になっている、といったたくさんの偶然が重なって、昨夕のシーンが生まれました。なんでもないときにふと自然が一瞬だけ奏でるハーモニー。これを見逃さない目、聞き逃さない耳を養うことは難しく、そしてとても大切に思います。
参考:
月・金星・木星の接近はなかなか起こらない(2017/11/17)
アーカイブ:2015年1月の金星と水星接近に関係する記事(ブログ内)