天体追尾速度の変化 ― 2024/07/27
何日か前に天文リフレクションズをパラパラめくっていたら、だいこもんさんのブログ「追尾速度と大気差:40年前の天文ガイド掲載の謎グラフをめぐる議論」なる記事が目に留まりました。キングスレート界隈の内容で、丁寧な解説と分析がとても面白いのでぜひお読みになってください。
現在の天体撮影は「細かく撮って、後で位置合わせしてスタックする」という方法が主流です。私自身はフィルム時代に「ひとコマ1時間を手動ガイド」みたいなころから経験を積んできたので、今の楽さ(落差?)が嘘のようですが、正確なガイドに関わる悩みは露出が変わっても今も昔も存在します。
ところで天体撮影しているみなさんは、左上画像のような“現象”に遭遇した経験はありませんか?これは2012年12月5日明け方の金星と水星の接近を85mm+APS-Cでとらえたもの。一見して普通のスナップ画像ですが、拡大すると違和感に気付くでしょう。恒星像のうち、上辺近くは点像なのに、下辺近く(かなり低空)は縦に伸びているのです。この画像は上方向が天頂向き、(敢えて真ん中ではなく)上辺近くの左右二点を基準にステライメージで15コマスタックしたもの。露出の最初と最後で約8.5分経過しています。
私たちが普段見ている星々は、既に大気差により真の位置から少し浮いた結果です。このため天体は「自転軸に垂直に天球を輪切りにした円周上」を日周するのではなく、もっと複雑な曲線に沿って移動するのです。左上画像のような構図ではどんなに正確なガイドをしても天頂側と地面側とで大気差の出方に違いがあり、片方を合わせるともう片方は合いません。別の例を下A・B画像に掲載しておきました。(※いずれも180mm+APS-C/フラット・ダーク処理は省略/インターバルが一定ではないため、伸びている星に途切れが生じてますがご容赦を。)月や惑星、彗星はそれ自身が独自に動くけれど、ここで問題にしてるのは「相互の位置関係が変わらないはずの恒星もずれが生じる」ことです。
個人的に低空の彗星などを積極的に撮影してきたため「大気差で画像内に伸びが生じる」経験は山ほどありました。露出が長引くほど顕著です。厄介なのは、低空撮影では写野内にガイド星が設定できないことがしばしばあり、一発撮りのフィルムでは星像全体が伸びてしまいました。今なら小刻みに撮れば目標天体近くを基準に位置合わせできますから、被害は最小限で済むのですが…。
おそらく同様の悩みはプロの観測者にもあったことでしょう。撮影が短時間で済んだり広写野なら気にならなくても、「フィルムによる長焦点・超長時間露光」なら話は別。対象の高度が変わると大気差の影響が出てしまい、画面に伸びが発生します。ちょうど移動する彗星を止めて撮影するために「彗星核でガイド撮影する」ようなことが、実は天頂以外の大部分の天体について必要です。
この難題をメカニカルな発想で打開しようとしたのがEdward Skinner Kingさんでした。対象高度に応じてモーター速度を変化させたり、大気で変化する日周の軌跡を「意図的に極軸をずらして」近似コースを追尾させるといった手法(King's method)です。さすがに追尾中に極軸を滑らかに変化させる機構は難しく、「極軸を故意にずらすガイド撮影」を積極的に取り入れているケースは少ないと思いますが、ガイド星のずれを見ながら極軸アラインメントする方法なら今も多くの方が利用しますね。「南天中空の星をガイドして南にずれるなら極軸を東にずらして…」みたいな呪文を暗記したことはありませんか?ソフトウェアに組み込まれた極軸合わせツールなどもこうしたドリフト法を精密にやっているに過ぎません。これを逆転の発想で「この星の日周は大気差でずれるので、最初から望遠鏡もずれて追いかけるよう極軸をずらし、追尾速度も変化させよう」というのがKingさんのアイディア原点なのでしょう。
今はもっぱらモーター速度の最適化のみがKing's rateとして広まってるようです。なお、海外の資料やサイトではtracking rateやguide rateという表現はあってもKing's rateという言い方は見たことがありません。和製英語でしょうか。
恒星に準じる天体(太陽系天体以外の遠方の対象)を赤道儀で撮影するとき、一般には「恒星時」という速度で回転するモーターを使います。約23時間56分4秒(=86164秒)で360°回転する、いわゆる恒星の日周運動の速度です。太陽の場合は平均24時間(=86400秒)で子午線に戻る「太陽時」。月や惑星、彗星、小惑星などは恒星に対して複雑な移動をするため、これらを正確に追尾するには別の方法が必要ですが、今回は省略。これらに対し、キングスレートは86190秒で一周する速度です。
冒頭で紹介しただいこもんさんのブログ記事には、対象天体の赤緯に応じた追尾速度の変化がグラフで紹介されています。このうち最初のSWATさんのグラフは以前に拝見しており、また40年前の天ガの記事も朧げな記憶が残っています。というのも、ちょうど当時所有していたアスコの赤道儀SX260に「大気差補正追尾回路」が組み込まれ、がっつり使っていたからです。取説にも大気差補正の表や図が載っていたように記憶しています。
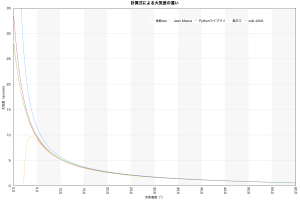
追尾速度グラフの肝となる大気差の近似式はいくつも考えられており、例えばwikiの日本語版と英語版を見ただけでも良く使われる式が幾つも書いてあります。日本語版のほうの式は長沢工さんの名著「天体の位置計算」に掲載されているものと同じですね。天文計算のバイブルで有名なJean Meeusさんの「Astronomical Algorithms」に載ってるのは英語版wiki:Sæmundsson's formulaと同等、また私がプログラミングで使っているPythonライブラリのものは同じく英語版wiki:Bennett's formulaと同等でした。いくつかピックアップしてグラフを描くと高度15°付近から下は差が出ますが、それより高ければほぼ一緒でした(右上図)。(※日本語版に載ってるJAVAプログラムは一部間違いがあるようですから気を付けてください。)
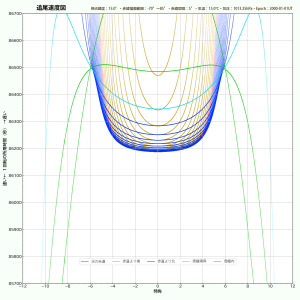
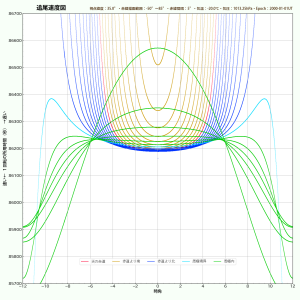
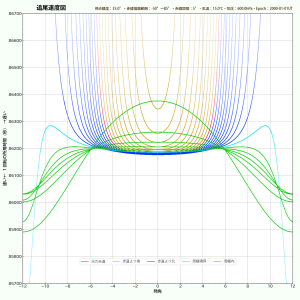
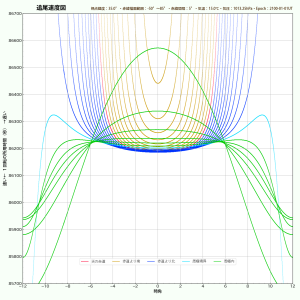
だいこもんさんのブログ記事にある追尾速度図(修正版)を、私なりに自作プログラムで描いてみました。(値が少し異なるのは大気差の計算式が違うからと思われます。)ついでに「パラメータの何を変えるとグラフはどう変化するか」という比較もしてみました。下にいくつかのサンプルを掲載しておきますので、ぜひ比べてみてください。全部同じサイズなのでフォトショ・レイヤー重ねで比較可能。基準(下C図)は観測地緯度が北緯35°、気温15度、1気圧です。各図のキャプションにあるdec0の数値は「天の赤道(図の赤線)と子午線(時角0hの縦線)の交点の追尾速度」、またalt45のほうは「高度45°と子午線の交点の追尾速度」です。これらはキングスレートに近いけれど、条件によって変化します。
また計算Epochを設定しました。刻々と動いている座標原点(=春分点)を基準に天体位置(瞬時の分点における視位置)を指定すると不都合が生じやすいため、星図・星表に示された位置は通常J2000.0といった基準分点が世界的に統一されています。今回グラフ化した各々の「赤緯」も2000年分点に統一しましたから、年月が経てば「視赤緯」が変化→同じ星でも高度方位が変わるのです。従って、グラフを計算する日付(=Epoch)はとても重要です。
こうしてみると、だいこもんさんのブログ記事にある修正前のグラフも、本質的には間違っていないんじゃないかと思えます。前提は分かりませんが、描いた当時の大気差算出データや観測地・環境設定によってグラフに幅が出ますからね。当然ながら追尾速度グラフは観測地緯度によって変化し、また大気差も気温や気圧、気体成分などで変わります。それどころか観測波長でも違いますから、例えば日本から数時間かけてオメガ星団(日本経緯度原点から高度1°以上に4.8時間ほど見える)をRGB分解撮影すると、再合成の位置合わせに大変苦労するでしょう。単純な伸び縮みに収まらないからです。無論、一晩中気温・気圧が一定なんてありえませんから、大気差補正追尾の完全自動化は困難と思われます。オフアキとか小型ガイド鏡で追いかけたほうがよほど簡便で正確です。それでもこうした大気差や追尾速度の原理的なところを知っておくのはとても大切に思います。(※追尾速度の分布を天球に投影した場合は2024年8月9日記事「天体追尾の遅速マップを描く」をご覧ください。)
参考:見かけの自転速度に関する記事
大気差を受けた北極星はどう動く?(2024/08/25)
天体追尾の遅速マップを描く(2024/08/09)
天体追尾速度の変化(2024/07/27)
現在の天体撮影は「細かく撮って、後で位置合わせしてスタックする」という方法が主流です。私自身はフィルム時代に「ひとコマ1時間を手動ガイド」みたいなころから経験を積んできたので、今の楽さ(落差?)が嘘のようですが、正確なガイドに関わる悩みは露出が変わっても今も昔も存在します。
ところで天体撮影しているみなさんは、左上画像のような“現象”に遭遇した経験はありませんか?これは2012年12月5日明け方の金星と水星の接近を85mm+APS-Cでとらえたもの。一見して普通のスナップ画像ですが、拡大すると違和感に気付くでしょう。恒星像のうち、上辺近くは点像なのに、下辺近く(かなり低空)は縦に伸びているのです。この画像は上方向が天頂向き、(敢えて真ん中ではなく)上辺近くの左右二点を基準にステライメージで15コマスタックしたもの。露出の最初と最後で約8.5分経過しています。
私たちが普段見ている星々は、既に大気差により真の位置から少し浮いた結果です。このため天体は「自転軸に垂直に天球を輪切りにした円周上」を日周するのではなく、もっと複雑な曲線に沿って移動するのです。左上画像のような構図ではどんなに正確なガイドをしても天頂側と地面側とで大気差の出方に違いがあり、片方を合わせるともう片方は合いません。別の例を下A・B画像に掲載しておきました。(※いずれも180mm+APS-C/フラット・ダーク処理は省略/インターバルが一定ではないため、伸びている星に途切れが生じてますがご容赦を。)月や惑星、彗星はそれ自身が独自に動くけれど、ここで問題にしてるのは「相互の位置関係が変わらないはずの恒星もずれが生じる」ことです。
個人的に低空の彗星などを積極的に撮影してきたため「大気差で画像内に伸びが生じる」経験は山ほどありました。露出が長引くほど顕著です。厄介なのは、低空撮影では写野内にガイド星が設定できないことがしばしばあり、一発撮りのフィルムでは星像全体が伸びてしまいました。今なら小刻みに撮れば目標天体近くを基準に位置合わせできますから、被害は最小限で済むのですが…。
おそらく同様の悩みはプロの観測者にもあったことでしょう。撮影が短時間で済んだり広写野なら気にならなくても、「フィルムによる長焦点・超長時間露光」なら話は別。対象の高度が変わると大気差の影響が出てしまい、画面に伸びが発生します。ちょうど移動する彗星を止めて撮影するために「彗星核でガイド撮影する」ようなことが、実は天頂以外の大部分の天体について必要です。
この難題をメカニカルな発想で打開しようとしたのがEdward Skinner Kingさんでした。対象高度に応じてモーター速度を変化させたり、大気で変化する日周の軌跡を「意図的に極軸をずらして」近似コースを追尾させるといった手法(King's method)です。さすがに追尾中に極軸を滑らかに変化させる機構は難しく、「極軸を故意にずらすガイド撮影」を積極的に取り入れているケースは少ないと思いますが、ガイド星のずれを見ながら極軸アラインメントする方法なら今も多くの方が利用しますね。「南天中空の星をガイドして南にずれるなら極軸を東にずらして…」みたいな呪文を暗記したことはありませんか?ソフトウェアに組み込まれた極軸合わせツールなどもこうしたドリフト法を精密にやっているに過ぎません。これを逆転の発想で「この星の日周は大気差でずれるので、最初から望遠鏡もずれて追いかけるよう極軸をずらし、追尾速度も変化させよう」というのがKingさんのアイディア原点なのでしょう。
今はもっぱらモーター速度の最適化のみがKing's rateとして広まってるようです。なお、海外の資料やサイトではtracking rateやguide rateという表現はあってもKing's rateという言い方は見たことがありません。和製英語でしょうか。
恒星に準じる天体(太陽系天体以外の遠方の対象)を赤道儀で撮影するとき、一般には「恒星時」という速度で回転するモーターを使います。約23時間56分4秒(=86164秒)で360°回転する、いわゆる恒星の日周運動の速度です。太陽の場合は平均24時間(=86400秒)で子午線に戻る「太陽時」。月や惑星、彗星、小惑星などは恒星に対して複雑な移動をするため、これらを正確に追尾するには別の方法が必要ですが、今回は省略。これらに対し、キングスレートは86190秒で一周する速度です。
冒頭で紹介しただいこもんさんのブログ記事には、対象天体の赤緯に応じた追尾速度の変化がグラフで紹介されています。このうち最初のSWATさんのグラフは以前に拝見しており、また40年前の天ガの記事も朧げな記憶が残っています。というのも、ちょうど当時所有していたアスコの赤道儀SX260に「大気差補正追尾回路」が組み込まれ、がっつり使っていたからです。取説にも大気差補正の表や図が載っていたように記憶しています。
追尾速度グラフの肝となる大気差の近似式はいくつも考えられており、例えばwikiの日本語版と英語版を見ただけでも良く使われる式が幾つも書いてあります。日本語版のほうの式は長沢工さんの名著「天体の位置計算」に掲載されているものと同じですね。天文計算のバイブルで有名なJean Meeusさんの「Astronomical Algorithms」に載ってるのは英語版wiki:Sæmundsson's formulaと同等、また私がプログラミングで使っているPythonライブラリのものは同じく英語版wiki:Bennett's formulaと同等でした。いくつかピックアップしてグラフを描くと高度15°付近から下は差が出ますが、それより高ければほぼ一緒でした(右上図)。(※日本語版に載ってるJAVAプログラムは一部間違いがあるようですから気を付けてください。)
だいこもんさんのブログ記事にある追尾速度図(修正版)を、私なりに自作プログラムで描いてみました。(値が少し異なるのは大気差の計算式が違うからと思われます。)ついでに「パラメータの何を変えるとグラフはどう変化するか」という比較もしてみました。下にいくつかのサンプルを掲載しておきますので、ぜひ比べてみてください。全部同じサイズなのでフォトショ・レイヤー重ねで比較可能。基準(下C図)は観測地緯度が北緯35°、気温15度、1気圧です。各図のキャプションにあるdec0の数値は「天の赤道(図の赤線)と子午線(時角0hの縦線)の交点の追尾速度」、またalt45のほうは「高度45°と子午線の交点の追尾速度」です。これらはキングスレートに近いけれど、条件によって変化します。
また計算Epochを設定しました。刻々と動いている座標原点(=春分点)を基準に天体位置(瞬時の分点における視位置)を指定すると不都合が生じやすいため、星図・星表に示された位置は通常J2000.0といった基準分点が世界的に統一されています。今回グラフ化した各々の「赤緯」も2000年分点に統一しましたから、年月が経てば「視赤緯」が変化→同じ星でも高度方位が変わるのです。従って、グラフを計算する日付(=Epoch)はとても重要です。
こうしてみると、だいこもんさんのブログ記事にある修正前のグラフも、本質的には間違っていないんじゃないかと思えます。前提は分かりませんが、描いた当時の大気差算出データや観測地・環境設定によってグラフに幅が出ますからね。当然ながら追尾速度グラフは観測地緯度によって変化し、また大気差も気温や気圧、気体成分などで変わります。それどころか観測波長でも違いますから、例えば日本から数時間かけてオメガ星団(日本経緯度原点から高度1°以上に4.8時間ほど見える)をRGB分解撮影すると、再合成の位置合わせに大変苦労するでしょう。単純な伸び縮みに収まらないからです。無論、一晩中気温・気圧が一定なんてありえませんから、大気差補正追尾の完全自動化は困難と思われます。オフアキとか小型ガイド鏡で追いかけたほうがよほど簡便で正確です。それでもこうした大気差や追尾速度の原理的なところを知っておくのはとても大切に思います。(※追尾速度の分布を天球に投影した場合は2024年8月9日記事「天体追尾の遅速マップを描く」をご覧ください。)
- 自作プログラムによる計算です。北半球の空を前提としています。
- 対象天体の位置がJ2000.0(ほぼICRS)で分かっているとして、指定元期に指定観測位置・指定観測環境から見たとき大気差で浮き上がり込みの移動量を算出。ひとつの赤緯ごと時角一周ぶんの「時角方向成分のみの追尾速度」を図化しました。
- 通常の速度は「距離/時間」や「角度/時間」のように表しますが、ここでの縦軸は「時間/一周」として逆数にしています。日周で一回転するのに何秒かかるか、と表現したほうがガイドレートの議論として分かりやすいためです。
- 無視できるほど微小ですが、実際は赤緯方向の移動もあります。
- プログラムの仕方によっては子午線付近に特異点が出てしまうことがありますが、今回は微小エラーを除外せず描いています。
- ちなみに図Jの600hPaはすばる望遠鏡のあるハワイ・マウナケア山頂近くの気圧です。(気温その他は違います。)
参考:見かけの自転速度に関する記事
大気差を受けた北極星はどう動く?(2024/08/25)
天体追尾の遅速マップを描く(2024/08/09)
天体追尾速度の変化(2024/07/27)